How to Determine Whether a Relation is a Function: A Comprehensive Guide
🤔 What’s a Function Anyway?
In the world of mathematics, a function is a special type of relation that assigns a unique output to each input. In simpler terms, it’s a fancy way of saying that for every value of "x" you throw at the function, it only spits out one value of "y." It’s like a one-way street where inputs go in, and specific outputs come out.
☝️ So, How Do I Know if a Relation is a Function?
Well, my friend, it’s all about the vertical line test. Brace yourself for a little bit of geometry:
- Draw your relation as a bunch of points on a graph.
- Take a ruler or your trusty finger and draw a vertical line anywhere you like.
- If the vertical line crosses any point more than once, you’ve got a problem. It’s not a function!
- If the line only crosses each point once, then congratulations! You’ve got yourself a function.
💁♂️ Vertical Line Test: A Picture is Worth a Thousand Words
Source www.showme.com
In this example, the vertical line crosses each point only once, making this relation a function.
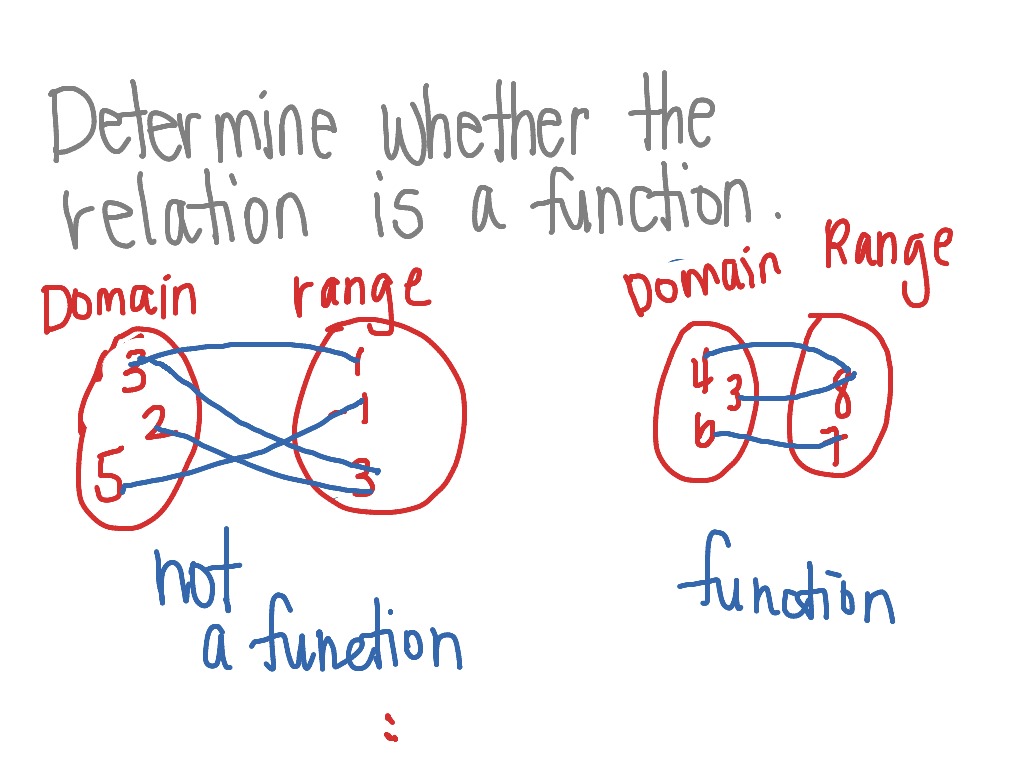
📝 What Makes a Relation Not a Function?
Sometimes, relations behave badly and break the rules. Here’s why:
- Bad Input: If a relation has the same input values paired with different outputs, it’s a no-go zone for functions. Example: (x, 1) and (x, 2) are different outputs for the same input "x."
- Bad Output: Functions demand uniqueness! If an input value yields more than one output, it’s not a function. Example: (x, 5) and (x, 7) are both outputs for input "x."
🤓 Examples of Functions and Non-Functions
Let’s play "Guess the Function":
Example 1:
- (1, 2), (3, 4), (5, 6), (7, 8)
- Function? Yes! Each input (1, 3, 5, 7) has a unique output (2, 4, 6, 8).
Example 2:
- (0, 4), (0, 7), (2, 6), (3, 2)
- Function? Nope! Input 0 has two different outputs (4 and 7).
✨ Functions in the Wild: Real-Life Applications
Functions aren’t just confined to math books; they’re everywhere! Here’s how you might encounter them in the real world:
- Distance Formula in Physics: The distance traveled by an object is a function of time.
- Profit Graph in Economics: The profit earned by a business is a function of the number of units sold.
- Weather Forecast: The temperature predicted for a given day is a function of the day of the year.
📚 Comparison Time: Function vs. Not a Function
Let’s put it all together with a handy comparison table:
| Characteristic | Function | Non-Function |
|---|---|---|
| Vertical Line Test | Crosses each point only once | Crosses some points more than once |
| Input-Output Relation | Each input has a unique output | Some inputs have multiple outputs |
| Common Example | Distance traveled as a function of time | Profit earned as a function of units sold with different prices |
✏️ Practice Makes Perfect: Test Yourself
Feeling confident? Test your function-detecting skills with these questions:
- Is the relation {(1, 2), (3, 2), (5, 6)} a function?
- Determine if the relation {(0, 0), (0, 1), (2, 4)} is a function.
- Is the relation {(-2, 5), (-1, 2), (0, 5)} a function?
Answers:
- No
- Yes
- Yes
🌟 Conclusion: You Got This!
Determining whether a relation is a function is a piece of cake if you master the vertical line test. Remember, every input should have its own special output, and if it doesn’t, it’s not a function. Be sure to check out our other awesome articles to expand your mathematical horizons even further!
FAQ about Determining if a Relation is a Function
1. What is a function?
A function is a relation that assigns to each element of a set (the domain) exactly one element of another set (the range).
2. How do I know if a relation is a function?
You can use the vertical line test:
- If any vertical line intersects the graph of the relation more than once, the relation is not a function.
3. What is the domain of a function?
The domain of a function is the set of all possible input values.
4. What is the range of a function?
The range of a function is the set of all possible output values.
5. Can a function have multiple outputs for the same input?
No, a function can only have one output for each input.
6. Can a relation be a function if it is not graphed?
Yes, you can still determine if a relation is a function using the definition or by examining the table of values.
7. What is the inverse of a function?
The inverse of a function is another function that reverses the input and output values.
8. How do I find the inverse of a function?
To find the inverse of a function, you can:
- Switch the roles of the input and output variables.
- Solve the resulting equation for the new output variable.
9. What is a one-to-one function?
A one-to-one function is a function where each input value corresponds to a unique output value.
10. Is the relation {(1, 2), (3, 4), (5, 6), (7, 2)} a function?
No, this relation is not a function because the input value 2 has two different output values (2 and 6).